Please show your calculationsclearly

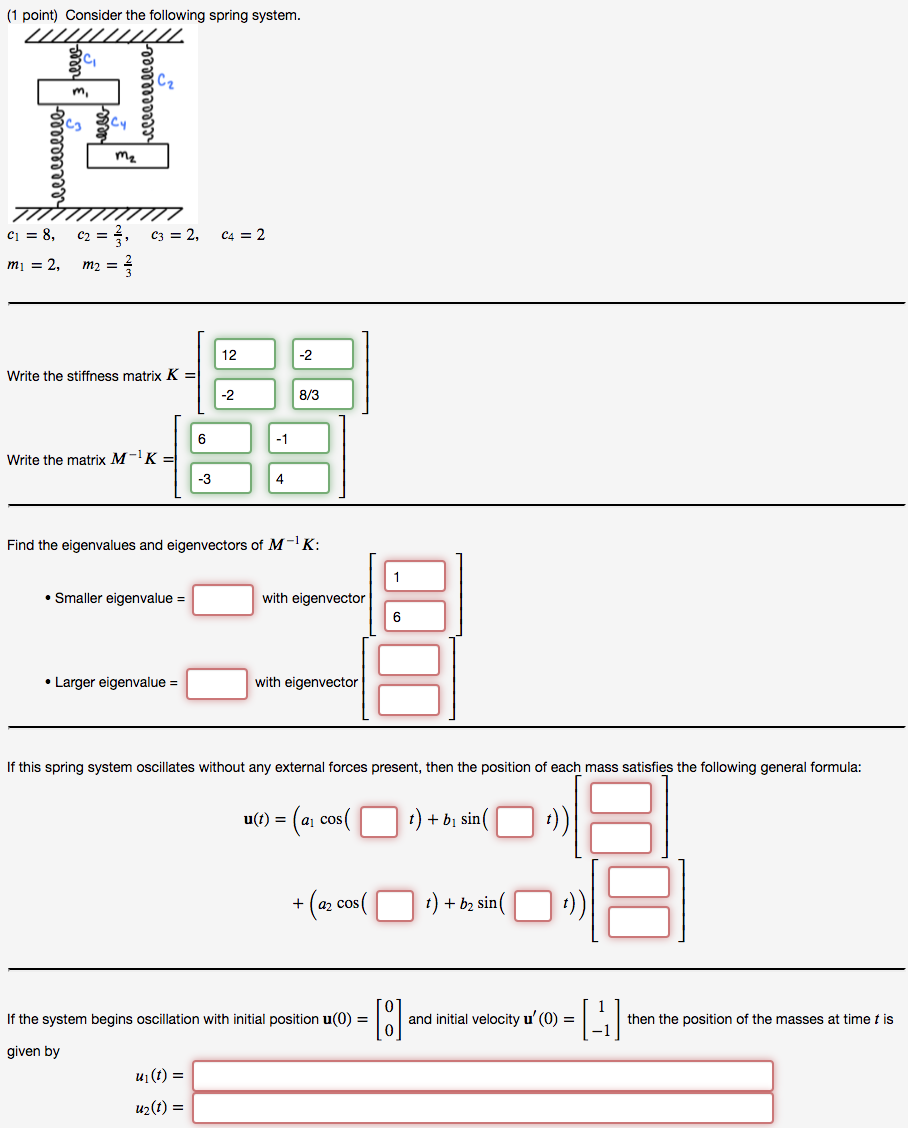
(1 point) Consider the following spring system. U2 UN mi 1000331 C3 C4 = 2 ci = 8, C2 = }; c3 = 2, m = 2, m2 = 12 -2 Write the stiffness matrix K = -2 8/3 6 -1 Write the matrix M-?K= -3 4 Find the eigenvalues and eigenvectors of M-K: 1 • Smaller eigenvalue = with eigenvector 6 • Larger eigenvalue = with eigenvector If this spring system oscillates without any external forces present, then the position of each mass satisfies the following general formula: u(t) = (a cos ( t) + b sin +(az cos ( t) + b2 sin ( 8 If the system begins oscillation with initial position (0) = O] and initial velocity u' (0) = -) then the position of the masses at time t is given by ui(t) = uz(t) =