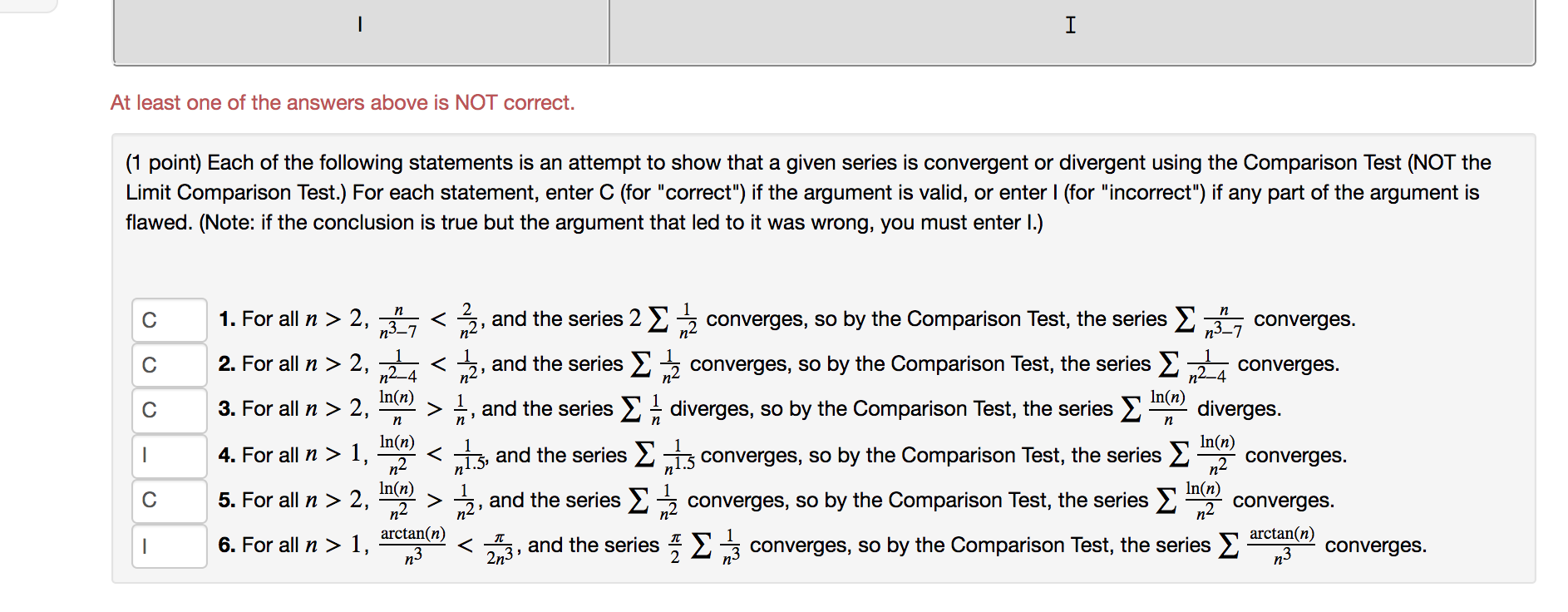
I At least one of the answers above is NOT correct. (1 point) Each of the following statements is an attempt to show that a given series is convergent or divergent using the Comparison Test (NOT the Limit Comparison Test.) For each statement, enter C (for "correct") if the argument is valid, or enter I (for "incorrect") if any part of the argument is flawed. (Note: if the conclusion is true but the argument that led to it was wrong, you must enter I.) n С с In(n) с In(n) n > n 1. For all n > 2, n3_7 < 2, and the series 2 E 2 converges, so by the Comparison Test, the series „, converges. 2. For all n > 2, < , and the series E converges, so by the Comparison Test, the series Enza converges. 3. For all n > 2, and the series 2 . diverges, so by the Comparison Test, the series E diverges. 4. For all n > 1, „T.s , and the series E „Is converges, so by the Comparison Test, the series 5. For all n > 2, > 2, and the series in converges, so by the Comparison Test, the series 2 6. For all n > 1, and the series 5Σ, converges, so by the Comparison Test, the series In(n) 1 < In(n) с In(n) n2 converges. In(n) converges. arctan(n) converges. n3 n2 arctan(n) TI 2n n-