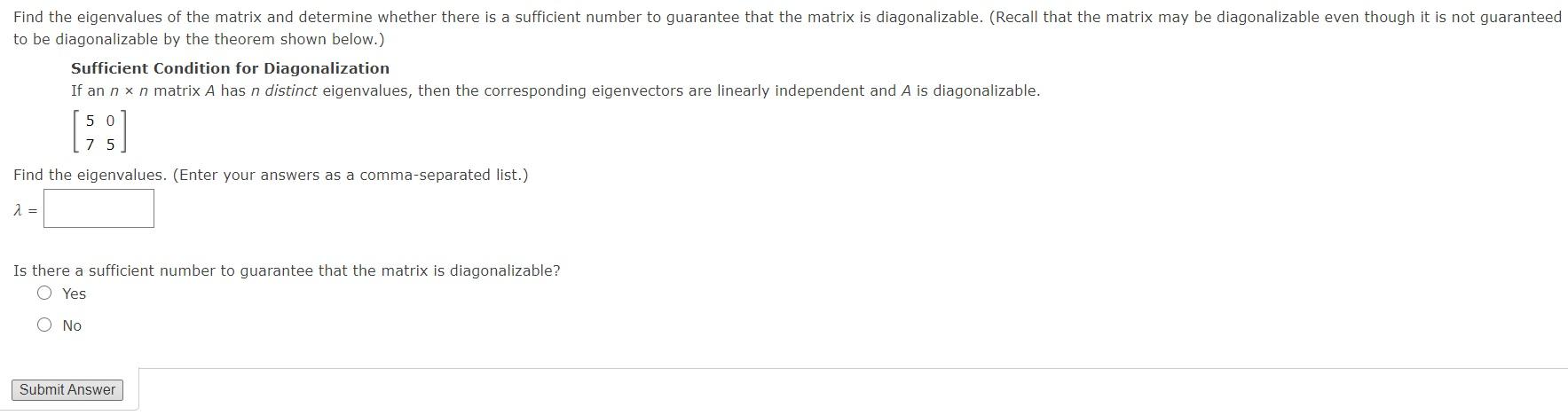
Find the eigenvalues of the matrix and determine whether there is a sufficient number to guarantee that the matrix is diagonalizable. (Recall that the matrix may be diagonalizable even though it is not guaranteed to be diagonalizable by the theorem shown below.) Sufficient Condition for Diagonalization If an n x n matrix A has n distinct eigenvalues, then the corresponding eigenvectors are linearly independent and A is diagonalizable. 5 0 75 Find the eigenvalues. (Enter your answers as a comma-separated list.) Is there a sufficient number to guarantee that the matrix is diagonalizable? O Yes O No Submit Answer