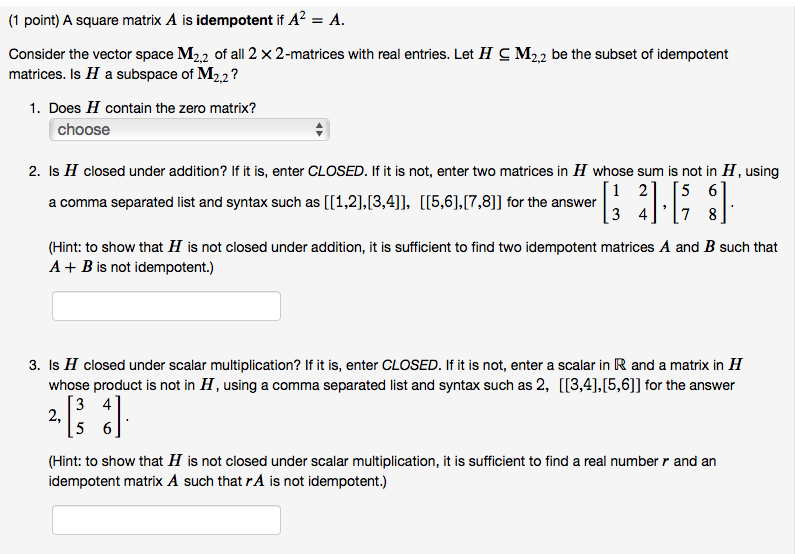
(1 point) A square matrix A is idempotent if A2 = A. Consider the vector space M2,2 of all 2 x 2-matrices with real entries. Let HCM2,2 be the subset of idempotent matrices. Is H a subspace of M2,2? 1. Does H contain the zero matrix? choose 2. Is H closed under addition? If it is, enter CLOSED. If it is not, enter two matrices in H whose sum is not in H, using 1 2 5 6 a comma separated list and syntax such as [[1,2],[3,4]], [[5,6],[7,8]] for the answer 3 8 [ #] [> :) (Hint: to show that H is not closed under addition, it is sufficient to find two idempotent matrices A and B such that A + B is not idempotent.) 3. Is H closed under scalar multiplication? If it is, enter CLOSED. If it is not, enter a scalar in R and a matrix in H whose product is not in H, using a comma separated list and syntax such as 2, [[3,4],[5,6]] for the answer 3 4 2, 5 6 (Hint: to show that H is not closed under scalar multiplication, it is sufficient to find a real number r and an idempotent matrix A such that rA is not idempotent.)
4. Is H a subspace of the vector space V? ✓ choose H is a subspace of V H is not a subspace of V ote: im all answers must be correct.