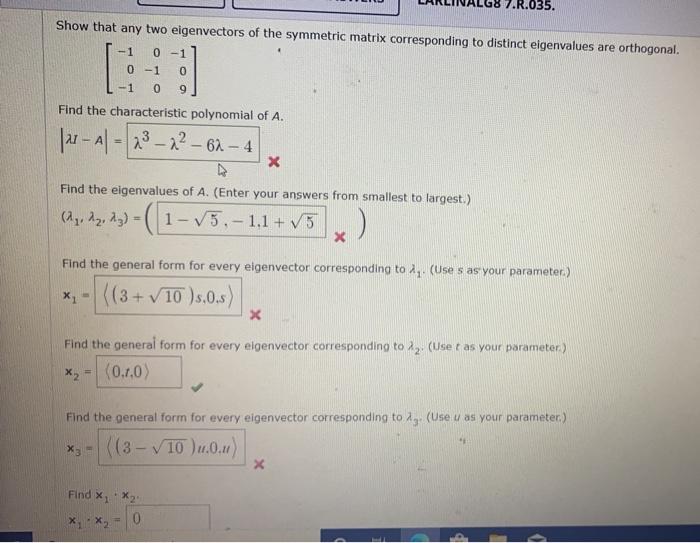
7.R.035. Show that any two eigenvectors of the symmetric matrix corresponding to distinct eigenvalues are orthogonal. 0-1 0-1 0 0 9 Find the characteristic polynomial of A. 1 - Al - 23 – 2² – 62 - 4 Find the elgenvalues of A. (Enter your answers from smallest to largest.) (1, 42, 43) - ( 1-15.-1.1 + V5 x) * - Find the general form for every elgenvector corresponding to in. (Uses as your parameter.) ((3 + V10 )s.0.5) X Find the general form for every elgenvector corresponding to iz: (Use t as your parameter) (0.1.0) *2 = Find the general form for every eigenvector corresponding to (Use u as your parameter.) 1( (3-√10 ) u.0.1) X Find,
11. [0/3 Points] DETAILS PREVIOUS ANSWERS LARLINALG8 Z.R.073. MY NOTES Use the age transition matrix L and the age distribution vector , to find the age distribution vectors x, and x, Then find a stable age distribution vector 03 16 1 0 800 0 L- 800 0 800 GO 0 19000 1000 500 х 13000 19000 500 Find a stable age distribution vector 18 5 1 Submit Answer