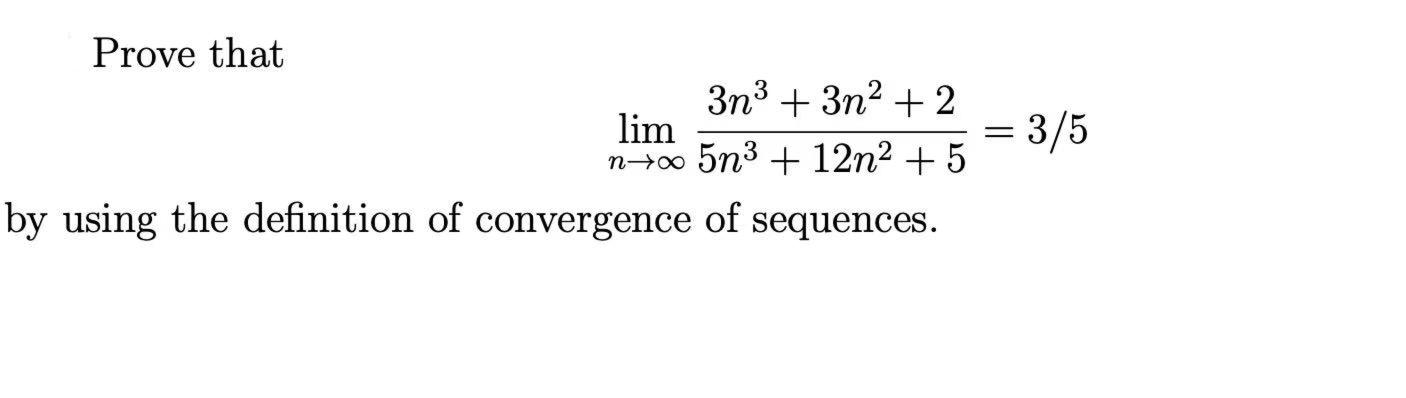
Prove that 3n3 + 3n2 + 2 lim = 3/5 n+ 5n3 + 12n2 + 5 by using the definition of convergence of sequences. 7.7 DEFINITION. Let E be a nonempty subset of R. A sequence of functions fr : E - R is said to converge uniformly on E to a function f (notation: fn → f uniformly on E as n + 0) if and only if for every e > 0 there is an N E N such that n> N implies \fn(x) – f(x) < € for all x EE. Comparing Definition 7.7 with Remark 7.2, we see that the only difference be- tween uniform convergence and pointwise convergence is that for uniform conver- gence, the integer N must be chosen independently of x (see Figure 7.2). Notice