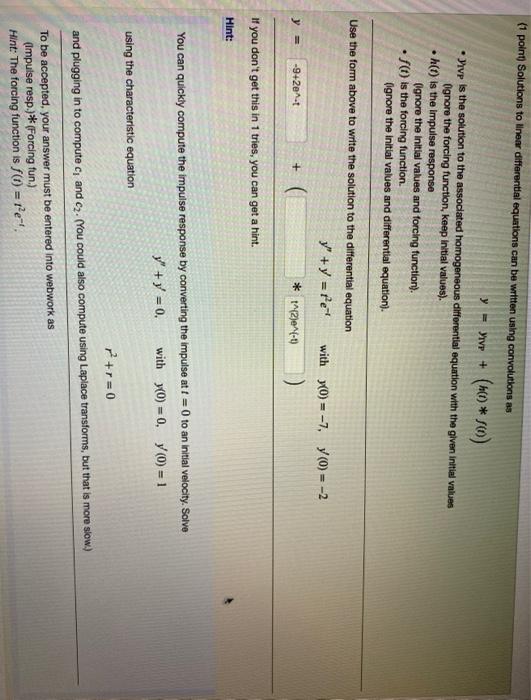
(1 point) Solutions to linear differential equations can be written using convolutions as y - Yvp + (HD *SO) • Pvp is the solution to the associated homogeneous differential equation with the given initial values ignore the forcing function, keep Initial values). h(t) is the Impulse response Ognore the initial values and forcing function). • f(is the forcing function. ignore the initial values and differential equation). Use the form above to write the solution to the differential equation y + y = fer with 30-7, 7(0) = -2 y = -942e^t + * 112)^(-0 If you don't get this in 1 tries, you can get a hint. Hint: You can quickly compute the impulse response by converting the impulse at t = 0 to an initial velocity. Solve y" + y = 0. with yO) = 0,0) = 1 using the characteristic equation p2 + r = 0 and plugging in to compute c, and c2. (You could also compute using Laplace transforms, but that is more slow.) To be accepted, your answer must be entered into webwork as (Impulse resp.)*(Forcing fun.) Hint: The forcing function is ) = re.