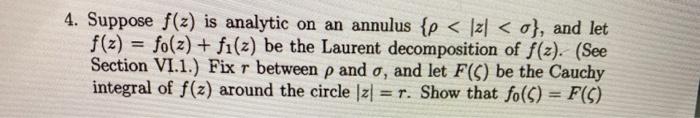4. Suppose F(z) Is Analytic On An Annulus {p < 121 < G}, And Let F(x) = Fo(z) + Fi(2) Be The Laurent Decomposition Of F(z). (See Section VI.1.) Fix R Between P And O, And Let F(C) Be The Cauchy Integral Of F(z) Around The Circle 1z| = R. Show That F
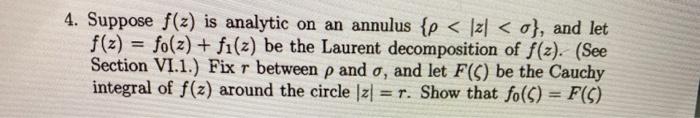
4. Suppose f(z) is analytic on an annulus {p < 121 < g}, and let f(x) = fo(z) + fi(2) be the Laurent decomposition of f(z). (See Section VI.1.) Fix r between p and o, and let F(C) be the Cauchy integral of f(z) around the circle 1z| = r. Show that fo(5) = F(C)
for 151 r. Show further that fo() = F-() and fi(5) = -F+(C). Remark. The formula f(x) = fo(z) + fi(2) reflects the jump theorem for the Cauchy integral of f(z) around circles z1 = r.