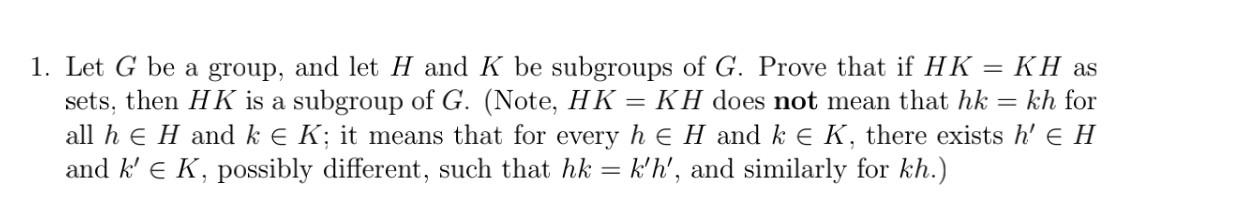
KH as = 1. Let G be a group, and let H and K be subgroups of G. Prove that if HK sets, then HK is a subgroup of G. (Note, HK = KH does not mean that hk kh for all h E H and ke K; it means that for every h E H and ke K, there exists h' e H and k' EK, possibly different, such that hk = k'h', and similarly for kh.)