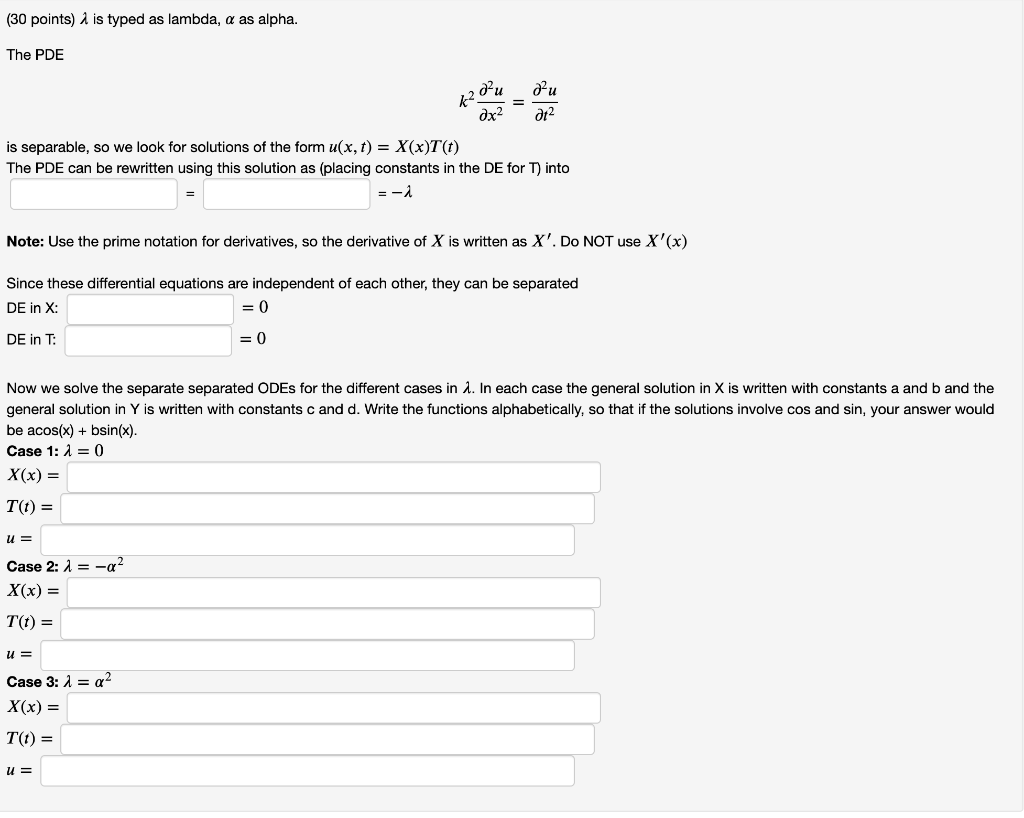
(30 points) 2 is typed as lambda, a as alpha. The PDE k2 du дх2 ди āt? is separable, so we look for solutions of the form u(x, t) = X(X)T(t) The PDE can be rewritten using this solution as (placing constants in the DE for T) into -2 Note: Use the prime notation for derivatives, so the derivative of X is written as X'. Do NOT use X'(x) Since these differential equations are independent of each other, they can be separated DE in X: =0 DE in T: = 0 Now we solve the separate separated ODEs for the different cases in 1. In each case the general solution in X is written with constants a and b and the general solution in Y is written with constants c and d. Write the functions alphabetically, so that if the solutions involve cos and sin, your answer would be acos(x) + bsin(x). Case 1: 1 = 0 X(x) = T(t) = U= Case 2:1 = -a? X(x) = T(t) = u = Case 3: 1 = a2 X(x) = T(t) = U=