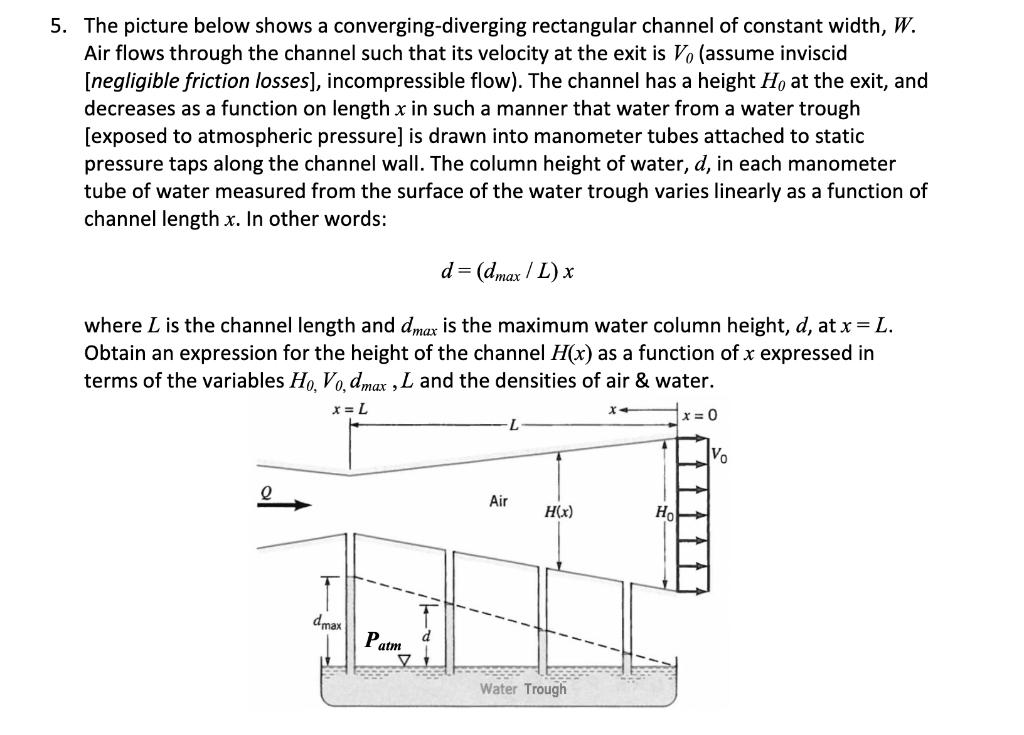
5. The picture below shows a converging-diverging rectangular channel of constant width, W. Air flows through the channel such that its velocity at the exit is V. (assume inviscid [negligible friction losses], incompressible flow). The channel has a height H, at the exit, and decreases as a function on length x in such a manner that water from a water trough [exposed to atmospheric pressure) is drawn into manometer tubes attached to static pressure taps along the channel wall. The column height of water, d, in each manometer tube of water measured from the surface of the water trough varies linearly as a function of channel length x. In other words: d=(dmax/L) x where L is the channel length and dmax is the maximum water column height, d, at x=L. Obtain an expression for the height of the channel H(x) as a function of x expressed in terms of the variables HQ, V, dmax ,L and the densities of air & water. x=L x = 0 L Vo Air H(x) HO dmax Patm Water Trough