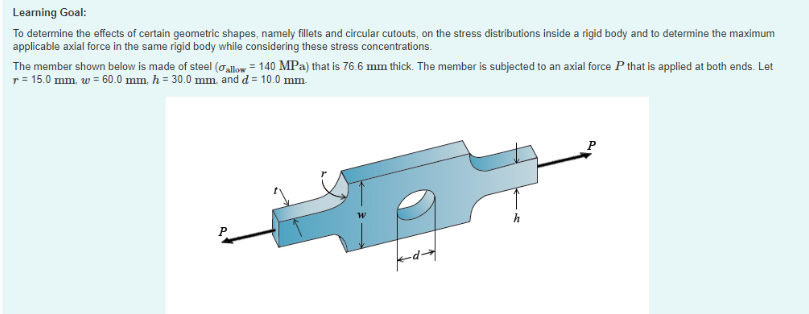
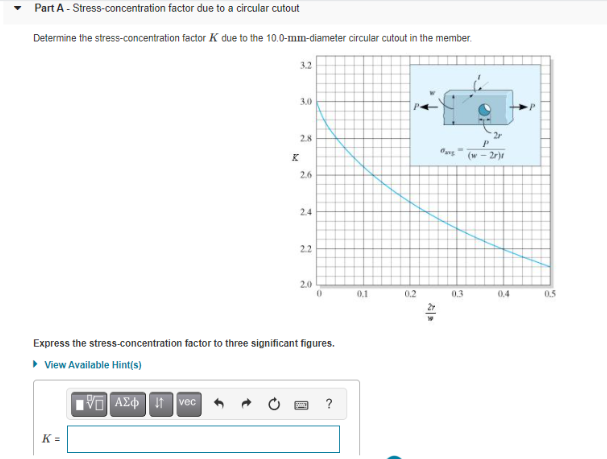
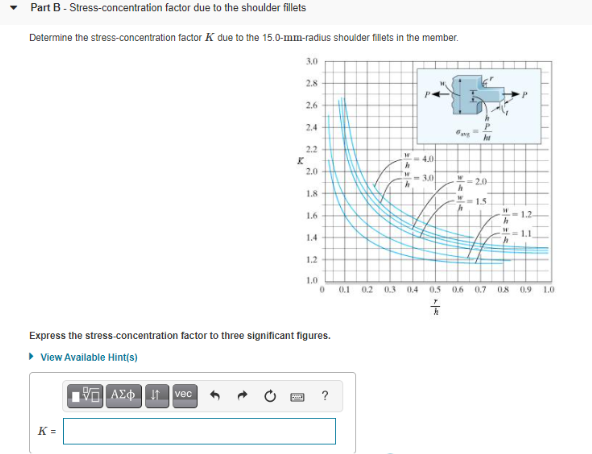
Learning Goal: To determine the effects of certain geometric shapes, namely fillets and circular cutouts, on the stress distributions inside a rigid body and to determine the maximum applicable axial force in the same rigid body while considering these stress concentrations. The member shown below is made of steel (O allow = 140 MPa) that is 76.6 mm thick. The member is subjected to an axial force P that is applied at both ends. Let r = 15.0 mm, w = 60.0 mm, h = 30.0 mm and d = 10.0 mm h P Part A - Stress-concentration factor due to a circular cutout Determine the stress-concentration factor K due to the 10.0-mm-diameter circular cutout in the member 32 3.0 28 K 2r11 26 2.4 2.2 2.0 0 0.1 02 03 0.4 05 Express the stress-concentration factor to three significant figures. View Available Hint(s) 190 AED 1 vec ? K= Part B - Stress-concentration factor due to the shoulder fillets Determine the stress-concentration factor K due to the 15.0-mm-radius shoulder fillets in the member. 10 2.8 2.6 2.4 2.2 - 4.0 2.0 H -30 18 15 1.6 h = 11 A 1.4 1.2 1.0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 08 09 LO Express the stress-concentration factor to three significant figures. View Available Hint(s) 190 AED! vec ? K = - Part C-Maximum applicable axial force P Using the information obtained about the stress-concentration factors in the member, determine the maximum applicable axial force P that can be applied to the member. Express the maximum applicable axial force in newtons to three significant figures. View Available Hint(s) | AEP Utvec ? P= N Submit Part D- Maximum applicable axial force P without the circular cutout Using the information obtained about the stress-concentration factors in the member, determine the maximum applicable axial force P that can be applied to the member if the circular cutout is not present Express the maximum applicable axial force in newtons to three significant figures. View Available Hints) 10 AED vec ? P= N Submit