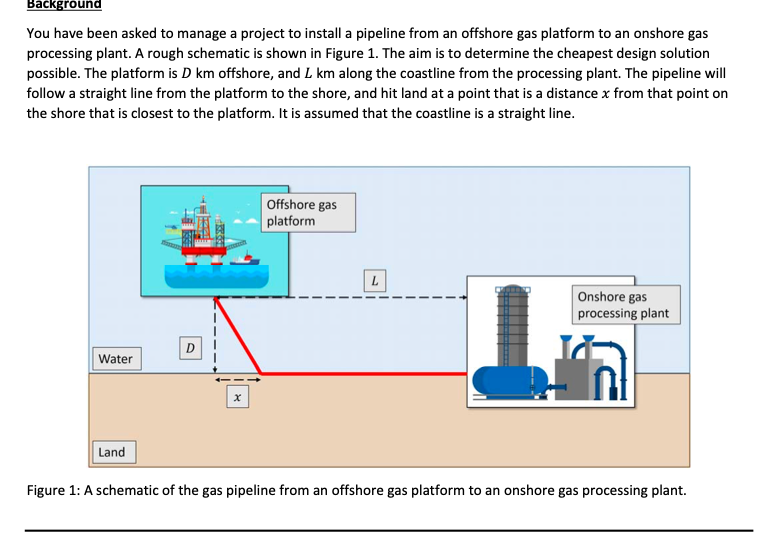
Background You have been asked to manage a project to install a pipeline from an offshore gas platform to an onshore gas processing plant. A rough schematic is shown in Figure 1. The aim is to determine the cheapest design solution possible. The platform is D km offshore, and L km along the coastline from the processing plant. The pipeline will follow a straight line from the platform to the shore, and hit land at a point that is a distance x from that point on the shore that is closest to the platform. It is assumed that the coastline is a straight line. Offshore gas platform L Onshore gas processing plant D Water an X Land Figure 1: A schematic of the gas pipeline from an offshore gas platform to an onshore gas processing plant.
Q1c In the Q1c.m file, use the Newton-Raphson method to determine the optimal value of x that corresponds to the minimum cost for each D value between 1 SD < 80km (increments of 1km) with L = 120km, Cs1 = $2.5 x 106/km and Coi = $2 x 106/km as per Q1a. In figure(4), produce a 2-by-1 subplot with the following: [Top subplot] Plot the optimal value of x against D [Bottom subplot] Plot the minimum cost against D