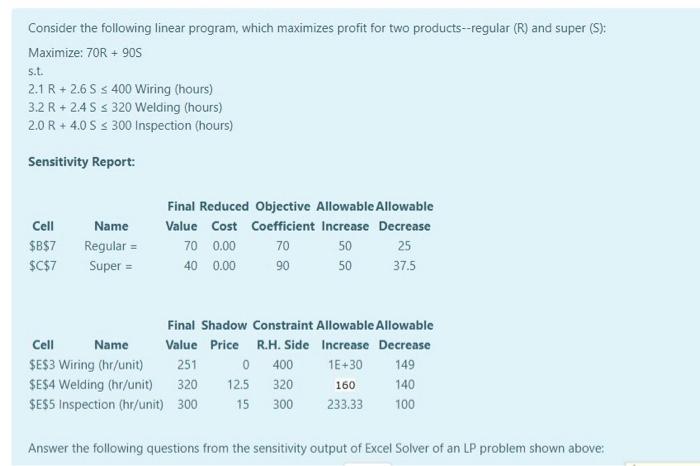
Consider the following linear program, which maximizes profit for two products--regular (R) and super (S): Maximize: 70R + 905 s.t. 2.1 R+ 2.6 S S 400 Wiring (hours) 3.2 R+ 2.4 S S 320 Welding (hours) 2.0 R + 4.0 S S 300 Inspection (hours) Sensitivity Report: Cell $B$7 $C$7 Name Regular = Super = Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 700.00 70 50 25 400.00 90 50 37.5 Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $E$3 Wiring (hr/unit) 251 0 400 1E+30 149 $E$4 Welding (hr/unit) 320 12.5 320 160 140 $E$5 Inspection (hr/unit) 300 15 300 233.33 100 Answer the following questions from the sensitivity output of Excel Solver of an LP problem shown above:
Answer the following questions from the sensitivity output of Excel Solver of an LP problem shown above: The optimal number of regular products to produce is and the optimal number of super products to produce is for total profits of $ ii) If the company wanted to increase the available hours for one of their constraints by two hours, they should increase i) The profit on the super product could increase by $ without affecting the product mix. iv) If downtime reduced the available capacity for wiring by 40 hours, the profit would be reduced by $ V) A change in the market has increased the profit on the super product by $5. Total profit will increase by vi) if the company wanted to decrease the available hours for one of their constraints by eight hours, they should decrease vii) The available slack in welding is vil) Shadow price of wiring remain O even if the R.H. Side is increased to infinity