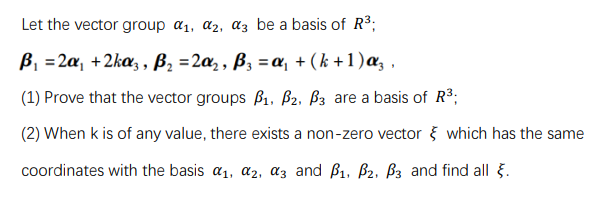
Let the vector group a1, az, a3 be basis of R3B1=2a1+2ka3,B2=2a2,B3=a1+(k+1)a3, (1)Prove that the vector groups B1, B2, B3 are a basis of R3; (2)When k is of any value, there exists non-zero vector which has the same coordinates with the basis a1, a2, a3 and B1, B2, B3 and find all 5.